[자료구조/Python] 해시(Hash), 해시테이블(Hash Table)

 

해당 포스팅은 [Do it! 자료구조와 함께 배우는 알고리즘 입문: 파이썬 편]과 [파이썬 알고리즘 인터뷰]을 통해 공부한 내용이 정리되어 있습니다.

---

해시/해쉬(Hash)란?

흔히 자료구조에서의 해시는 해시 테이블(Hash Table)을 뜻하며, Key와 Value로 어떠한 대응 관계를 나타내는 자료구조임

언어에 따라 해시, 맵, 사전 등으로 불리지만 파이썬에서는 딕셔너리 자료형을 통해 구현(충돌 시 오픈 어드레싱 방식을 사용)되어 있음

 

해시법(Hashing)

해시법은 '데이터를 저장할 위치 = 인덱스'를 간단한 연산으로 구현하는 것을 뜻함

다시 말해 해시 테이블을 인덱싱하기 위해 해시 함수를 사용하는 것!

• 원소의 검색, 추가·삭제를 모두 효율적으로 수행할 수 있음: O(1)

 

By Jorge Stolfi - Own work, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=6471238

 

우리는 해시 테이블의 인덱스를 구하기 위해 키를 해시값(hash value)으로 변환해야함

• 이때 사용하는 것이 해시 함수(hash function)!
  • 해시 함수: 임의 크기 데이터를 고정 크기 값으로 매핑하는 데 사용할 수 있는 함수
  • 성능 좋은 해시 함수들의 특징
    • 해시 함수 값 충돌의 최소화
    • 쉽고 빠른 연산
    • 해시 테이블 전체에 해시 값이 균일하게 분포
    • 사용할 키의 모든 정보를 이용하여 해싱
    • 해시 테이블 사용 효율이 높을 것

• 해시 테이블에서 실제 값이 저장되는 공간은 bucket(또는 slot)이라고 함
  • 데이터가 하나도 없는 버킷의 값은 None이라고 함

 

해시 테이블의 장단점

장점	단점
자료의 검색, 읽기, 저장 속도가 빠름 충돌이 발생하지 않았을 경우 O(1)	저장 공간을 미리 확보해야 함
자료의 중복 여부 체크가 쉬움	충돌을 해결할 방법이 필요

 

 

해시 충돌(Collision)

해시 충돌이란 변환된 해시값이 같아 저장할 버킷이 중복되는 현상을 뜻함

해시 테이블을 충분히 크게 만들면 충돌 발생을 억제할 수 있지만 메모리 낭비가 생김: 시간과 공간의 trade-off

따라서 충돌의 발생은 아래의 두 가지 방법을 통해 해결할 수 있음

• 개별 체이닝(Separate Chaining, 오픈 해시법 Open Hashing)
• 오픈 주소법(Open Addressing)

 

개별 체이닝(Separate Chaining)

개별 체이닝이란 해시값이 같은 데이터를 체인(chain) 모양의 연결 리스트로 연결(link)하는 방법을 뜻하며, 오픈 해시법(Open Hashing) 또는 체이닝(Chaining)이라고도 함

• 원래 해시 테이블 구조의 원형이기도 한 전통적인 방식 → 흔히 말하는 해시 테이블은 이 방식을 뜻함

 

이미지 출처: 파이썬 알고리즘 인터뷰 (이미지를 클릭하면 출처로 이동합니다)

1. 이미지에서는 윤아와 서현의 해시값이 동일하여 충돌이 발생
2. 윤아의 다음 아이템으로 서현을 연결해 연결 리스트 형태로 충돌을 해결함

장점: 충돌이 날 때 공간을 만들어 연결해주기 때문에 저장 공간을 효율적으로 사용할 수 있음

단점: 깊은 연결 리스트가 생길 경우 검색 효율이 떨어질 수 있음

 

오픈 주소법(Open addressing)

오픈 주소법(오픈 어드레싱)이란 충돌이 발생했을 때 탐사(probing)를 통해 빈 슬롯을 찾는 방법을 뜻하며, 닫힌 해시법(Closed Hashing)이라고도 함

 

이미지 출처: 파이썬 알고리즘 인터뷰 (이미지를 클릭하면 출처로 이동합니다)

• 앞서 살펴본 개별 체이닝 방법은 무한정으로 저장할 수 있지만, 오픈 어드레싱 방식은 전체 슬롯의 개수 이상은 저장할 수 없음
  • 일정 이상 채워지면(기준이 되는 로드 팩터 비율을 넘어서게 되면) Growth Factor의 비율에 따라 더 큰 크기의 또 다른 슬롯을 생성한 후 새롭게 복사하는 Rehashing 작업이 일어남

• 충돌 발생 시 테이블 공간 내에서 탐사를 통해 빈 슬롯을 찾아 해결하기 때문에 모든 원소가 반드시 자신의 해시값과 일치하는 주소에 저장된다는 보장이 없음
• 오픈 어드레싱의 가장 간단한 방식으로는 선형 탐사가 있음
  • Linear Probing: 충돌이 발생할 경우 해당 위치부터 순차적으로 탐사를 하나씩 진행함
    • 구현이 간단하면서도 성능이 좋은 편에 속하는 방법
    • 문제점: 해시 테이블에 저장되는 데이터들이 뭉치는 경향이 있음 → 클러스터링 Clustering
    • 이 클러스터가 점점 커지게 되면 인근 클러스터들과 서로 합쳐지는 일이 발생하고, 해시 테이블의 특정 위치에 데이터가 몰려 다른 위치에는 상대적으로 데이터가 거의 없는 상태가 될 수 있음
    • 이러한 클러스터링 현상은 탐사 시간을 오래 걸리게 하고, 전체적인 해싱 효율을 떨어뜨리는 원인이 됨

장점: 추가적인 데이터 구조를 이용하지 않기 때문에 메모리 사용량이 개별 체이닝에 비해 작을 수 있음

단점: 큰 로드 팩터에 민감함

 

로드 팩터(Load Factor)

로드 팩터란 해시 테이블에 저장된 데이터 개수 n을 슬롯의 개수 k로 나눈 것

• 로드 팩터를 통해 해시 함수를 재작성해야 될지, 또는 해시 테이블의 크기를 조정해야 할지를 결정
• 해시 함수가 키들을 잘 분산해 주는지를 판단하는 효용성 측정에도 사용
• 로드 팩터가 증가할수록 해시 테이블의 성능은 점점 감소하게 됨
• 파이썬의 로드 팩터는 0.66 (오픈 어드레싱 방식)

 

 

https://commons.wikimedia.org/wiki/File:Hash_table_average_insertion_time.png#/media/File:Hash_table_average_insertion_time.png

 

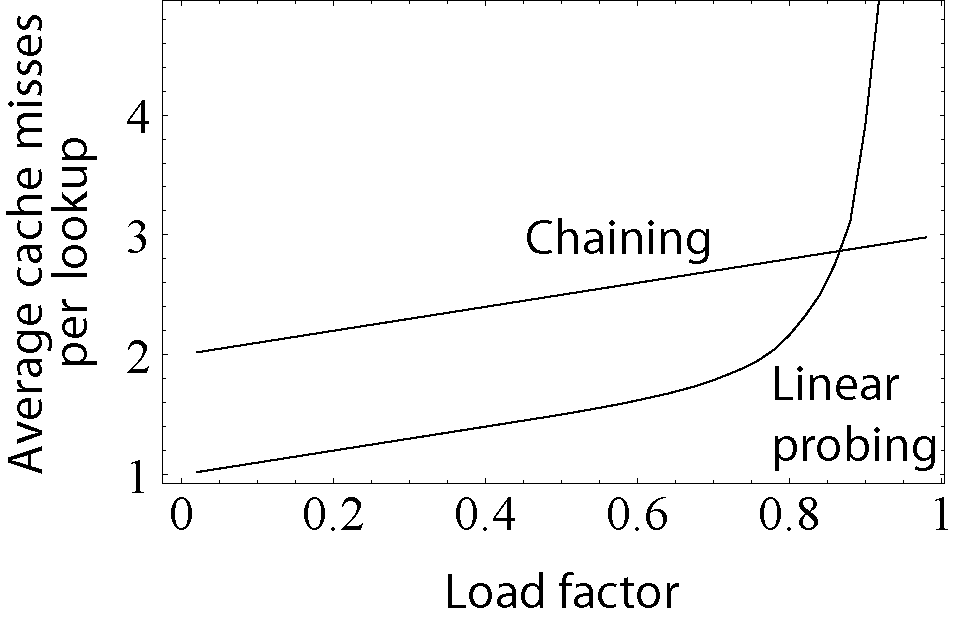
선형 탐사(오픈 어드레싱) 방식은 대체적으로 체이닝보다 좋은 성능을 내지만 슬롯의 80% 이상이 차게 되면 급격한 성능 저하가 발생

또한 체이닝과 달리 전체 슬롯의 전체 개수 이상, 즉 로드 팩터 1 이상은 저장할 수 없음

 

오류와 관련된 지적은 언제든 댓글로 달아주세요!